Reading notes: The Adaptive Radix Tree

4 July 2021

This time the paper is about a data structure implemented for HyPer, an in-memory database. The Adaptive Radix Tree, ART for short, has comparable performances of hash tables and maintains data in sorted order. This property allows to also perform efficient range queries.

Why the radix tree?

There are 3 kinds of data structures to maintain indexes in memory.

The first kind is the binary tree. T tree is old and not optimized for modern CPU architecture. B+ tree is more cache-friendly but tempers with the predictive comparison from modern CPU. FAST is great for modern CPU architectures, but it does not support incremental updates.

The second kind is the hash table. They are very efficient in memory indexes but only support single-point queries. Updates and deletion can be expensive when they require reorganizing the hash table.

The third and final kind of structure is the radix tree. The complexity of radix trees grows with the length of the key, not the number of elements in the structure. They suffer bad space performance when the keys are sparse.

ART uses 3 techniques to make radix tree a viable option:

• Dynamic node size
• Path compression
• Lazy expansion

Radix trees have good properties:

1. Complexity depends on key length, not the number of elements
2. There no need for rebalancing: two different insert orders result in the same tree
3. Keys are store in lexicographical order
4. Keys are implicitly stored in the path

The paper does not explain how the 4th property is useful. Given that keys are stored in the leaf nodes, I don't understand how implicit storing helps.

Dynamic node size

Inner nodes of the radix tree use a "span" s, they store 2^s pointers. So for a k-bit key, the height of the tree is k/s. Radix trees are smaller than binary trees if the number of elements n is n > 2^(k/s). For pure lookups, a higher span is better. But space usage is bad because most of the pointers are nulls.

ART uses a large span with different fanouts. When inserting, if the node is too small, it is replaced by a larger one. If underfull, the node is replaced with a smaller one.

They use a span of 8 bits to ease the implementation (the radix tree used in Linux uses a 6 bits span). Because changing the fanout of the node for every update operation would be counterproductive, They choose 4 different node sizes:

• Node4 is the smaller inner node, it contains a maximum of 4 children nodes stored as arrays
• Node16 is a larger Node4. For efficient lookup, it can use SIMD operations
• Node48 uses an indirection layer to store children node
• Node256 uses a single array of 2^span = 256 length

Leaf nodes use different representations:

1. Single value
2. Multiple values: same as inner nodes, but points to values instead of nodes
3. Combined pointer/value, using pointer tagging

I didn't understand this part. The paper does not follow up on implementation details of when these nodes are used. I simply ignored this

Lazy expansion

Lazy expansion and compressed path are useful for long keys. They highly reduce space consumption by skipping inner nodes.

Lazy expansion is when inner nodes are used for a single value. In the following diagram, it the case for key FOO:

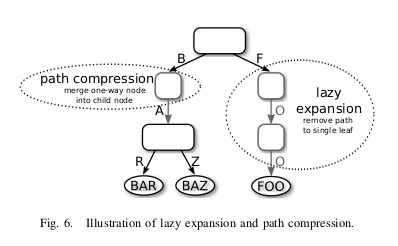
The key F in the root node points directly to the value. This allows for two inner nodes to be skipped. Since the full key is not stored in the inner nodes, the key is stored in the leaf node.

Path compression

Path compression has the same goal as the lazy expansion but in another setting. Inner nodes that point to a single child are removed. There are 2 ways to bridge the gap:

• Pessimistic: inner nodes contain the partial keys that were skipped. The lookup routine verifies the skipped key corresponds to the searched key
• Optimistic: the length of skipped keys is stored. The lookup routine verifies the key only once the leaf node is reached

The pessimistic approach leads to memory fragmentation: partial keys can be arbitrarily long. The author notes that a hybrid approach is possible. There are 8 keys skipped stored in a pessimistic fashion. The length of skipped keys is also stored. If there are more than 8 keys skipped, the lookup switches to an optimistic approach.

Conclusion

I won't cover the performance part of the paper, but globally it is very good. ART is excellent for sparse keys. Only hash tables compete. There are two possible evolutions:

• implement efficient concurrent updates with latch-free synchronization
• use another technique for dynamic node size that could be efficient on disk

This paper is crystal clear and fun. I don't know how I find out about it, but it certainly inspired people to implement Radix Tree. Like the Raft paper, it focuses on implementation while providing an intuitive explanation. Do read this paper, it is very enjoyable!

Take care